Updated On 195 To keep watching this video solution for FREE, Download our App Join the 2 Crores Student community now! Best Answer Suppose that we have an equation y=ax^2bxc whose graph is a parabola with vertex (3,2), vertical axis of symmetry, and contains the point (1,0)Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more
Www Cgsd Org Site Handlers Filedownload Ashx Moduleinstanceid 280 Dataid 1438 Filename 393 Smp Seaa C06l04 Pdf
What does b represent in ax^2+bx+c
What does b represent in ax^2+bx+c-You get these gems as you gain rep from other members for making good contributions and giving helpful advice #2 Report 6 years ago #2 ( Original post by differentiation) y=x^3ax^2bxc, where the curve touches the xaxis at x = 3 and x = 1Click here👆to get an answer to your question ️ The diagram shows the graph of y = ax^2 bx c , then Join / Login maths The diagram shows the graph of y = a x 2 b x c, then



Quadratic Graph Example Y Ax C Expii
Y ax 2 bx c x b b 2 4 ac2 a x b b 2 4 ac2 a this y = ax 2 bx c = x b √ b 2 4 ac 2 a x b √ b 2 4 ac 2 a This works with everything, although sometimes the root is complex ( C ) There are other ways Example 33 1Click here👆to get an answer to your question ️ The vertex of the parabola y = ax^2 bx c is Join / Login maths The vertex of the parabola y = a x 2 b x c is Answer y = a x 2 b x c The vertex will correspond to the point where the curve attains a minima (a > 0) or maxima (a < 0)Given and Also ⇒ We know that ⇒ Hence;
B is the coefficient of the y term c is the constant term the slopeintercept form of the equation of a straight line is y = mx b where m is the slope b is the yintercept to convert from the standard form of the equation of a straight line to the slopeintercept form of the equation for a straight line, solve for x ax by = c is the standard form subtract ax from both sides of thisGiven y = ax 2 bx c , we have to go through the following steps to find the points and shape of any parabola Label a, b, and c Decide the direction of the paraola If a > 0 (positive) then the parabola opens upward If a < 0 (negative) then the parabolaF"(a), f"(b), f"(c) are Given f(x) = ax 2 bx c ⇒ ⇒ So f"(a)= f"(b;
Y = ax 2 bx c In this exercise, we will be exploring parabolic graphs of the form y = ax 2 bx c, where a, b, and c are rational numbers In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the third We have split it up into three parts varying a only varying b only varying c onlyIn this case, a = 2, b = –4, and c = –3 Then the answer is x = –058, x = 258 , rounded to two decimal places Warning The "solution" or "roots" or "zeroes" of a quadratic are usually required to be in the "exact" form of the answer y = ax 2 bx c is a parabola In the following applet, you can explore what the a, b, and c variables do to the parabolic curve The effects of variables a and c are quite straightforward, but what does variable b do?



1



Www Humbleisd Net Cms Lib Tx Centricity Domain 3442 Quadratic formula word problems Pdf
Solution for ax^2bx=cy equation Simplifying ax 2 bx = c 1y Solving ax 2 bx = c 1y Solving for variable 'a' Move all terms containing a to the left, all other terms to the right Add '1bx' to each side of the equation ax 2 bx 1bx = c 1bx 1y Combine like terms bx 1bx = 0 ax 2 0 = c 1bx 1y ax 2 = c 1bx 1y Reorder the terms ax 2 = 1bx c 1y Divide If the polynomial `x^(3)ax^(2)bx30` is exactly divisible by `x^(2)2x15` Find a and b and also the third factor asked in Mathematics by Eshaan01 ( 714k points)Watch Video in App This browser does not support the video element



Http Faculty Uml Edu Bkim 22 1 Lecture 5 Matlab basic1 Pdf
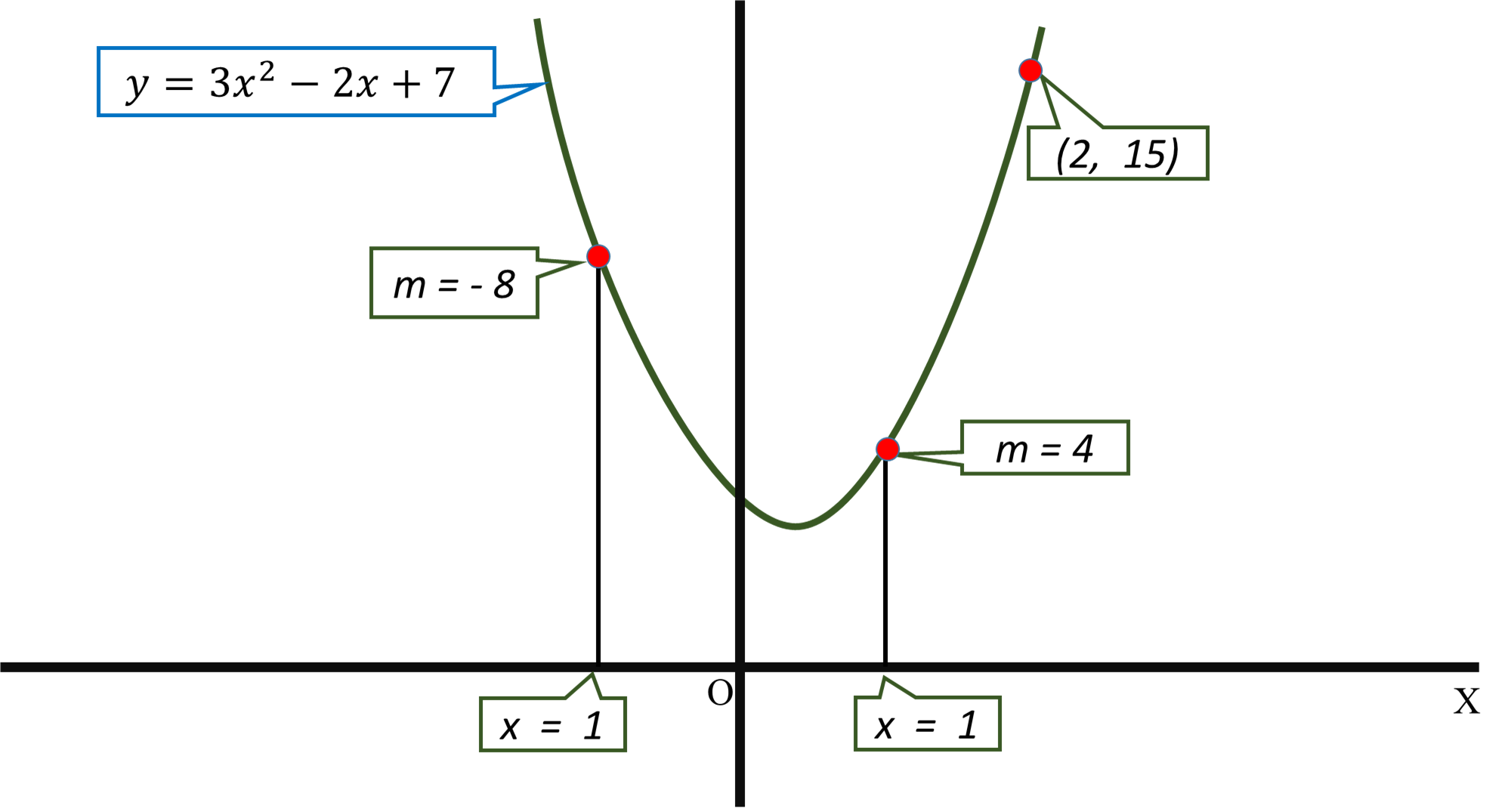



How Do You Find A Parabola With Equation Y Ax 2 Bx C That Has Slope 4 At X 1 Slope 8 At X 1 And Passes Through 2 15 Socratic
For more problems and solutions visit http//wwwmathplanetcom√1000以上 y=ax2 bx c equation What does y=ax2bxc mean Quadratic Formula Calculator What does y=ax2bxc mean What does y=ax2bxc meanGraphing A Parabola Of The Form Y Ax 2 Bx C Integer Coefficients Youtube How to Find the Axis ofSymmetry y = ax2 bx c The line for the axis of symmetry crosses over the number achieved by doing the formula –b/2a 9 Problem 1 Formula y = ax2 bx c y = 5x2 10x – 3 Directions find the vertex, yintercept



Observations Of Asymptotic Behavior




Graphing Y Ax 2 Bx C
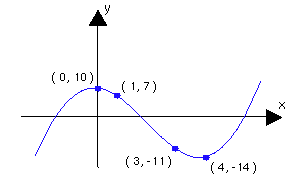
3 The curve y =ax 2 bx c passes through the point (2, 4) and is tangent to the line y = x 1 at (0, 1) Determine values for a, b, and c Gauss sits at the point (b –c, 4a)If then which one of the following is correct? If y=ax^(2)bxc passes through the points (3, 10), (0, 1), and (2, 15) , what is the value of abc ?



Assignment 2 By Shridevi Kotta This Write Up Explores Equation Of Parabola Y Ax2 Bx C We Observe That With B C 0 A Determines How The Parabola Is Oriented And The Curve Rises Fast Or Slow In Other Words How Narrow Or How Wide The Parabola Is At



View Question What Do A B And C Mean In Y Ax 2 Bx C
Answer provided by our tutors y= ax^2 bx c a) touches the xaxis at 4 and passes through (2,12) touches the xaxis at 4 means that passes trough (4,0) and b^2 4*a*c = 0 (the quadratic has 1 solution) passes trough (4,0) that is for x=4 y=0 4 = a*0^2 b*0 c c = 4 passes through (2,12) that is x = 2 and y = 12Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreThings to Do In this applet, you start with a simple quadratic curve (a parabola) You can investigate the curve as follows




Graphing Y Ax2 Bx C Youtube
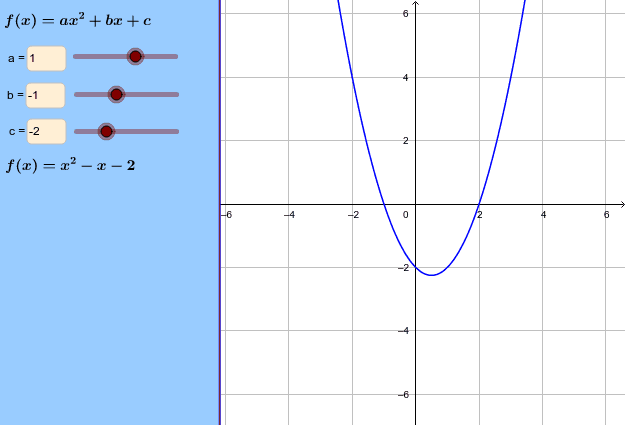



The Graph Of Y Ax 2 Bx C Geogebra
(1) a constant (2) a function of x only (3) a function of y only (4) a function of x and y Solution Given y 2 = ax 2 bx c Differentiate wrtx 2y dy/dx = 2ax b (i)I have this equation y = *x^*x And I would like to obtain the result of the equation when I give "y" numbers, edited explanation 2/06/ I want toA compound quadratic is a polynomial that can be expressed in the form a x 2 n b x n c ax^{2n}bx^{n}c a x 2 n b x n c, where a ≠ 0, b a \neq 0,b a = 0, b and c c c are constants, and n n n is a positive integer This can be generalized to compound polynomials, where the degree of the terms is a multiple of some positive integer



Www Cgsd Org Site Handlers Filedownload Ashx Moduleinstanceid 280 Dataid 1438 Filename 393 Smp Seaa C06l04 Pdf




54 The Graph Of Y Ax2 Bx C Is Shown In The Given Figu Scholr
5) The xcoordinate of the vertex is at b/2a The ycoordinate of this vertex is found by plugging in x = b/2a into ax^2 bx c Those aren't really handy for graphing, however What you do in practice if you want to graph ax^2 bx c is you complete the square You get it in the form a(xh)^2 y = ax² bx c y bx c = ax² x² x²(y/x²) (b/x) (c/x²) = a john1231 john1231 Mathematics High School answered Y = ax^2bxc, solve for a 1 See answer john1231 is waiting for your help Add your answer and earn points f(x)=ax^2bxc => f'(x)=2axb Remember that the derivative of a sum is the sum of the derivatives (y(x)g(x)z(x))'=y'(x)g'(x)z'(x) In this case f(x)=y(x)g(x)z(x



If Y Ax 2 Bx C Represents A Parabola With Vertex A As Shown In The Figure And B 2 2 B 2ac Sarthaks Econnect Largest Online Education Community




Consider The Graph Of A Quadratic Function Y Ax2 Bx C If B2 4ac
The equation of a curve is y = x^2 ax b where a and b are integers The points (0,5) and (5,0) lie on the curve Find the coordinates of the turning point of the curve In the equation for our line we have 2 unknowns a and bF'(a), f'(b), r(c) are in Given f(x) = ax 2 bx c ⇒ But b= 0 So I;Since ⇒ ⇒ = ⇒ ⇒ We kno



The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora
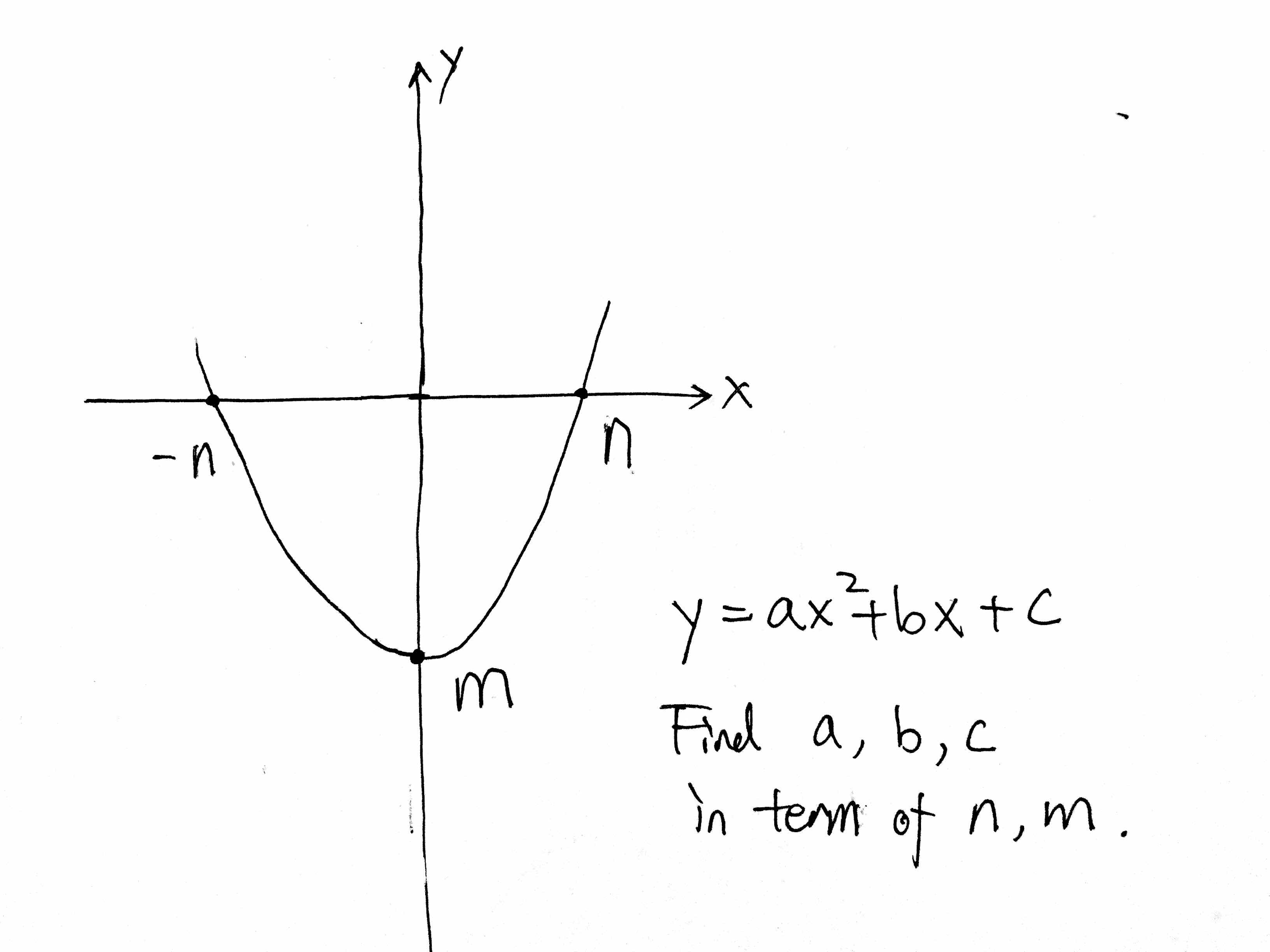



Y Ax 2 Bx C Find A B C In Term Of N M Chegg Com
The curve {eq}y = ax^2 bx c {/eq} passes through the point {eq}(1,6) {/eq} and is tangent to the line {eq}y = 4x {/eq} at the origin Find {eq}a, b, {/eq} and {eqConverting $y=ax^2bxc$ to $y=a(xh)^2k$ A quadratic equation in the form $\cl"red"{y=ax^2bxc}$ is said to be in standard form, while an equation in the form $\cl"blue"{y=a(xh)^2k}$ is said to be in vertex form In this section you will learn to convert equations such as $y=2x^22x3$ from standard form to vertex form A quadratic function is a function of the form y = ax 2 bx c, where a≠ 0, and a, b, and c are real numbers How does b affect the parabola?




The Equation For A Parabola Has The Form Y Ax 2 Bx C Where A B And C Are Constants Homeworklib




Activity 8 1 6 Exploring The Parameters Of Y Ax 2 Bx C
y = ax^2 bx c is a quadratic equation The vertex is located at (2, 5) and the graph opens up, this means that it never intercepts the x The second equation will come from taking the derivative of your original function \begin{align*} y &= ax^2 bx c \\ \frac{dy}{dx} &= 2ax b \end{align*} We know that since the relative max occurs at $(3,12)$ we know that $\frac{dy}{dx} = 0$ and $x = 3$ so plugging in we have $$ 0 = 6a b $$ So that results in our two equations being \begin{align*} 11 &= 9a 3b \\ 0 &= 6a bOf that vague equation, the X coordinate is at b/2a To find the Y coordinate, plug it back in Now if you would like to do this the calculus way, differentiate the equation, and set the resulting 2ax = b and solve for X Then, plug the X back




Answered 3 3 2 17 2 9 1 1 3 For The Graph Bartleby



A Tangent To A Quadratic
In the next few questions, we will find the roots of the general equation y = a x 2 b x with a ≠ 0 by factoring, and use that to get a formula for the axis of symmetry of any equation in that form Question 5 We want to factor a x 2 b x Because both terms contain an x, Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeRewrite the equation as ax2 bx c = y a x 2 b x c = y Move y y to the left side of the equation by subtracting it from both sides Use the quadratic formula to find the solutions Substitute the values a = a a = a, b = b b = b, and c = c−y c = c y into the quadratic formula and solve for x x Simplify the numerator



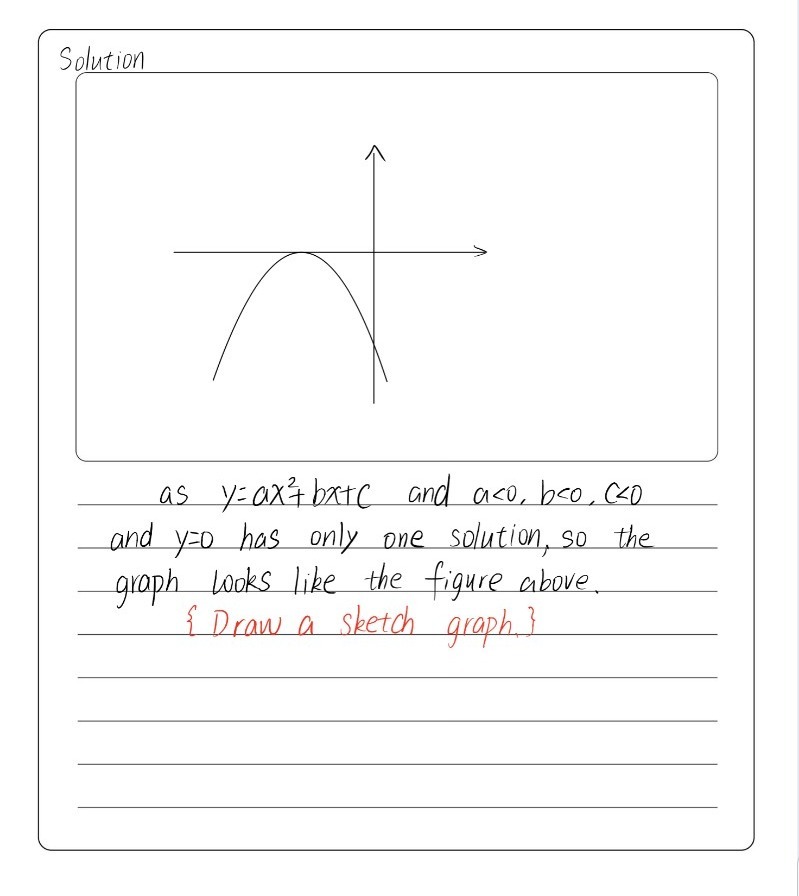
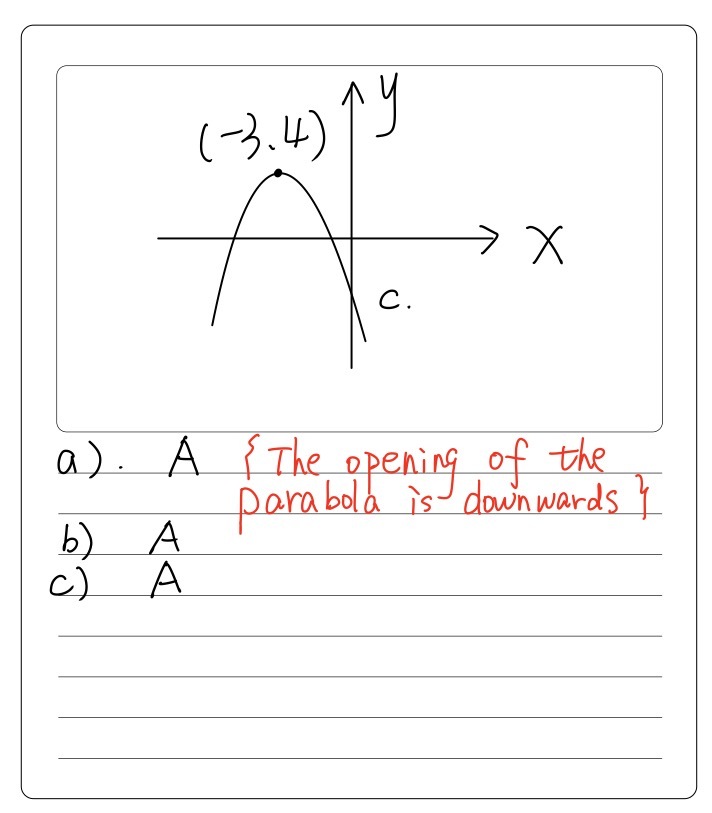
Solution Draw A Sketch Graph Of Y Ax 2 Bx C If A Lt 0 B Lt 0 C Lt 0 Discriminant 0
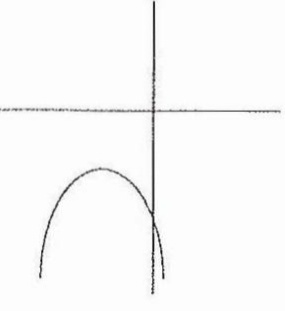



Above Is The Graph Of The Function Y Ax 2 Bx C Where A B 0 And C 0 Which Of The Graphs Below Could Be The Graph Of The Function Y Ax 2 Bx C A B C D E
We will learn how to find the maximum and minimum values of the quadratic Expression ax^2 bx c (a ≠ 0) When we find the maximum value and the minimum value of ax^2 bx c then let us assume y = ax^2 bx c Or, ax^2 bx c y = 0 Suppose x is real then the discriminant of equation ax^2 bx c y = 0 is ≥ 0 ie, b^2 4a(cWhen b = 0, the vertex of the parabola lies on the yaxis Changing b does not affect the shape of the parabola (as changing a did) Making b positive or negative only reflects the parabola across the yExplain Let us write the equation ax by = c in slope intercept form y = (a/b)x c/b The slope is given by (a/b) Set a, b and c to some values Drag the red markers so that they are on the line, read their coordinates and find the slope of the line Compare the slope found to (a/b)



Linear Algebra Webnotes Class Assignments Chapter 1




Graphing Y Ax 2 Bx C
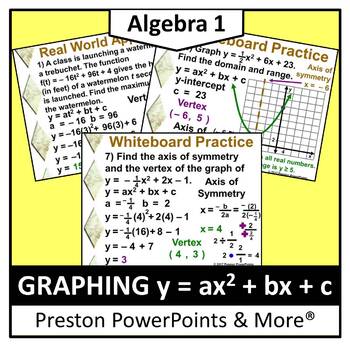
22 Y=A(1B^X) Power 23 Y=AX^(BX^C) Power^Power 24 Y=A(EXP(BX))C(EXP(DX)) Sum of Exponentials 25 Y=A(X^B)EXP(CX) Exponential Type 1 26 Y=(ABX)EXP(CX)D Exponential Type 2 27 Y=AB(EXP(C(XD)^2)) Normal 28 Y=A(B/X)EXP(C(LN(X)D)^2) Lognormal 29 Y=A Exp(BX) Exponential Y=ax^2bxc a 0Lv 7 1 decade ago IF small and large case letters have the same meaning within this queston then 1) "Y"or "y" represents the vertical axis value of a position/displacement vs time relationship The displacement of this motion has a parabolic graph shapeIf Y = Ax^2 Bx C is the position of the car the velocity is the derivative of this equation theThe Graph of y = ax2 bx c 393 Lesson 64 The Graph of y = ax2 bx c Lesson 6–4 2 BIG IDEA The graph of y = ax bx c, a ≠ 0, is a parabola that opens upward if a > 0 and downward if a < 0 Standard Form for the Equation of a Parabola Homer King hits a high–fl y



Draw A Sketch Graph Of Y Ax2 Bx C Where A 0 B 0 Gauthmath



Sat Math Grid Ins Question 97 Answer And Explanation Cracksat Net
Y = ax 2 bx c Move the loose number over to the other side y – c = ax 2 bx Factor out whatever is multiplied on the squared term Make room on the lefthand side, and put a copy of "a" in front of this spaceIf and then what is equal to?Given a quadratic function \(f(x) = ax^2bxc\), it is described by its curve \y = ax^2bxc\ This type of curve is known as a parabola A typical parabola is shown here Parabola,




Quadratic Graph Example Y Ax C Expii




The Adjoining Figure Shows The Graph Of Y Ax 2 Bx C Then Youtube
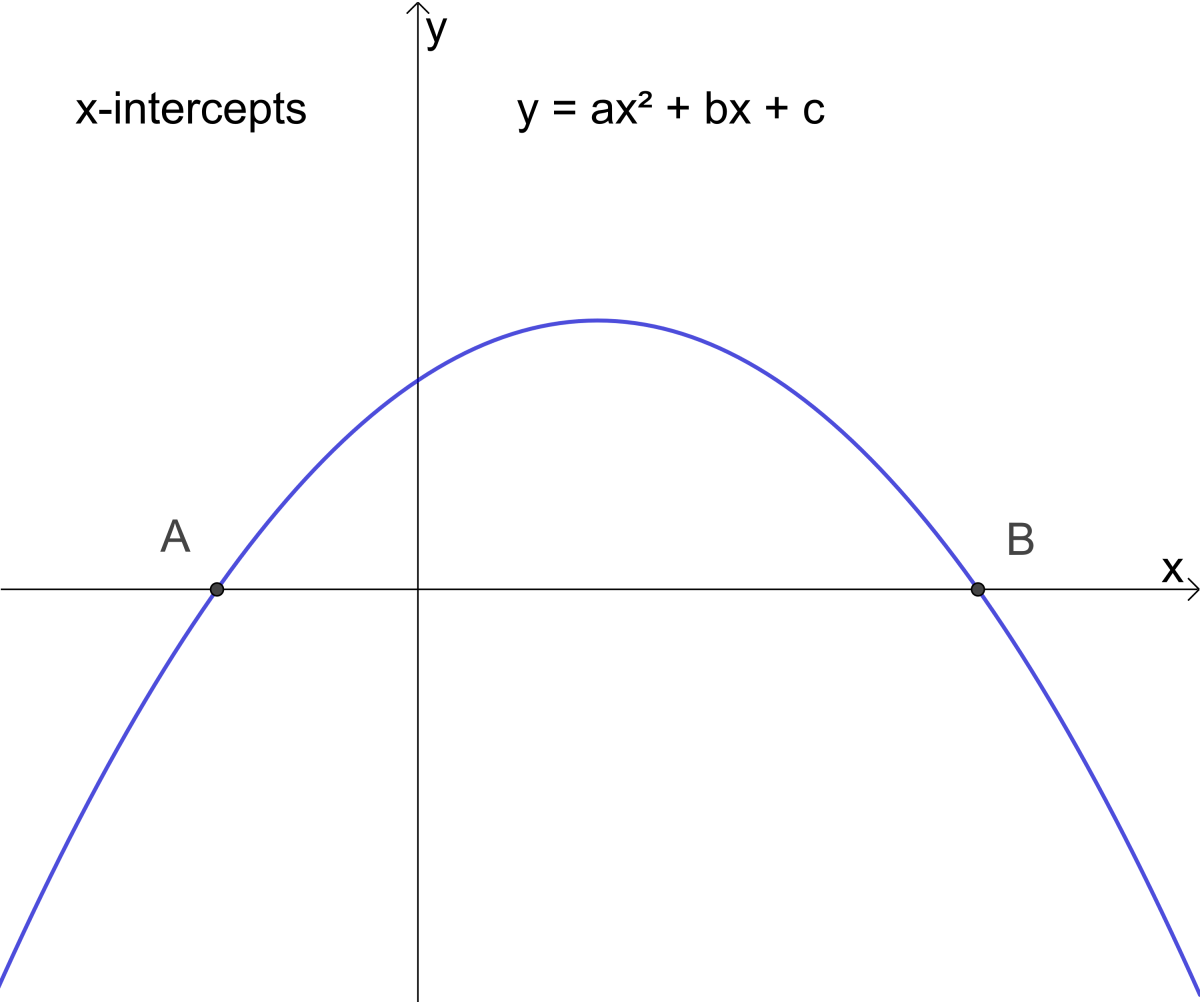
Integral of sqrt(ax^2 bx c) dxWatch more videos at https//wwwtutorialspointcom/videotutorials/indexhtmLecture By Er Ridhi Arora, Tutorials Point InIf the graph of the quadratic function \ (y = ax^2 bx c \) crosses the xaxis, the values of \ (x\) at the crossing points are the roots or solutions of the equation \ (ax^2 bx c = 0 \) If




Clockwise Markers For The Functions Linear Y Ax B Quadratic Y Download Scientific Diagram




Let F X Ax 2 Bx C Consider The Given Diagram Then



Alg 1 Graphing Y Ax2 Bx C In A Powerpoint Presentation Tpt



Sometimesmath Weebly Com Uploads 1 1 8 3 1129 Graphing Ax 5e2 Bx C Pdf




2 The Graph Of Y Ax2 Bx C Passes Through The Point Gauthmath




Which Of The Following Is An Equation In The Form Y Ax2 Bx C Of The Parabola Shown In The Brainly Com




Quadratic Formula Calculator




How Do You Find A Quadratic Function F X Ax 2 Bx C For Which F 1 2 F 3 46 And F 3 16 Socratic



Math Spoken Here About Quadratics 3



Unique Quadratic Equation In The Form Y Ax 2 Bx C




Y Ax2 Bx C Solution



Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Owlcation




Given That F X Ax 2 B X C And F X Y F X F Y Xy For Problem Solving Ps



A Sketch Of Y Ax2 Bx C Is Shown B The Maximum Poi Gauthmath



Math Spoken Here About Quadratics 3




B Value Definition Explanation Video Lesson Transcript Study Com



How To Determine A Quadratic Function Y Ax 2 Bx C If Its Graph Passes Through The Point 2 19 And It Has A Horizontal Tangent At 1 8 Quora



Q Tbn And9gcskitjvtu4g6u7oh5r8z42jlb391urt3idlmfdbjguuxli7v2fo Usqp Cau
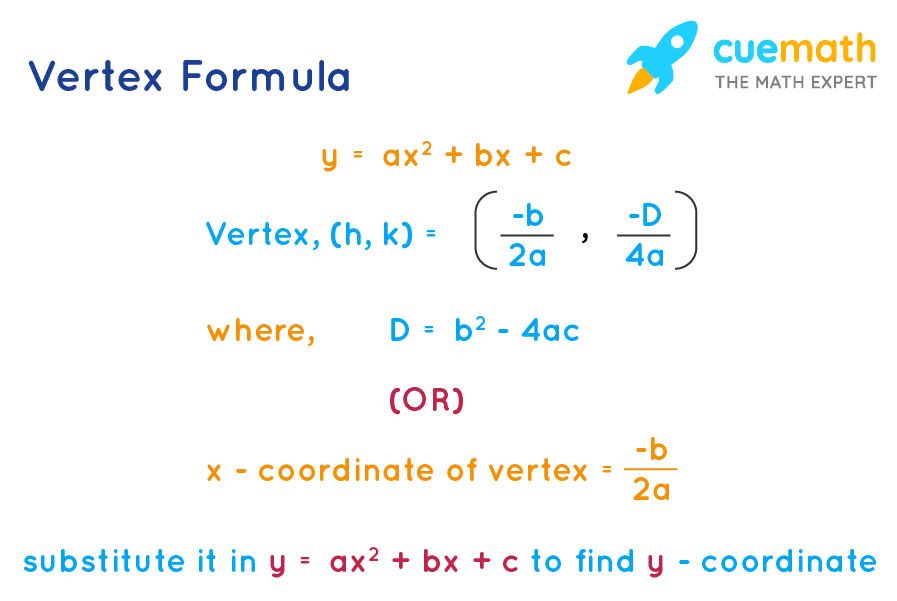



Vertex Formula What Is Vertex Formula Examples
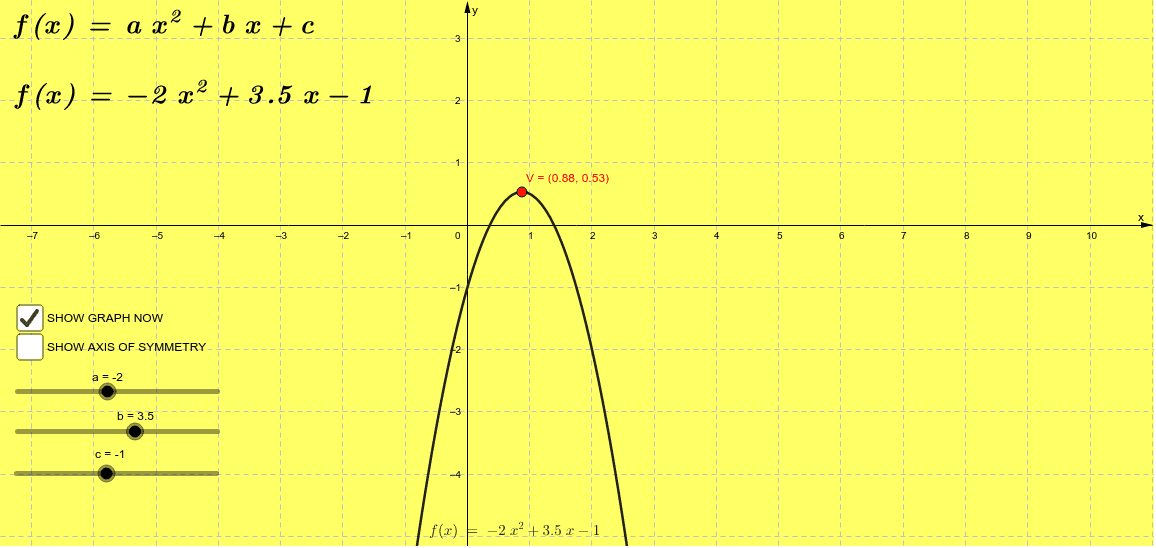



The Quadratic Function Y Ax2 Bx C Geogebra



1
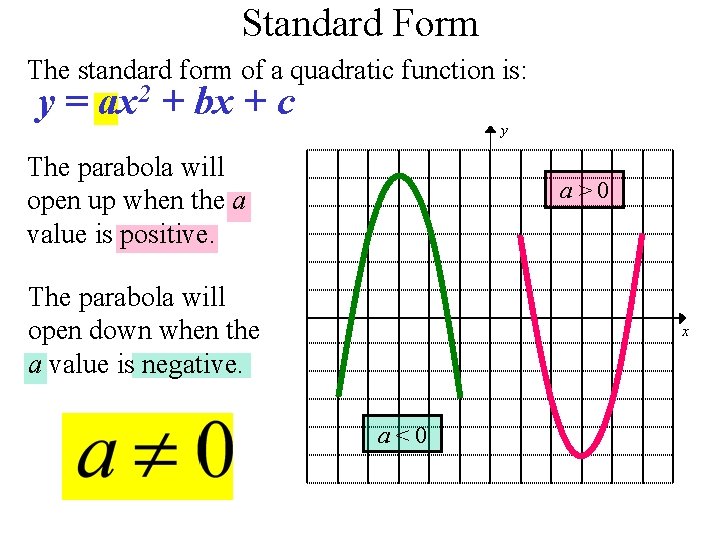



Quadratic Function Y Ax 2 Bx C Quadratic



Linear Algebra Webnotes Class Assignments Chapter 1



Exploring Parabolas Y Ax 2 Bx C




Quadratic Equation Wikipedia




The Sketch Is The Curve Of Y Ax2 Bx C Find A B And C




Missing C Value Quadratics




The Graphs Of Y Ax 2 Bx C Are Given In The Figure Identify The Signs Of Maths Polynomials Meritnation Com




A Sketch Of Y Ax Bx C Is Shown The Maximum Point Is 3 4 Select The Correct Answer In Each Brainly Com




Find An Equation In The Form Y Ax 2 Bx C For The Parabola Passing Through The Points Brainly Com



Quadratics
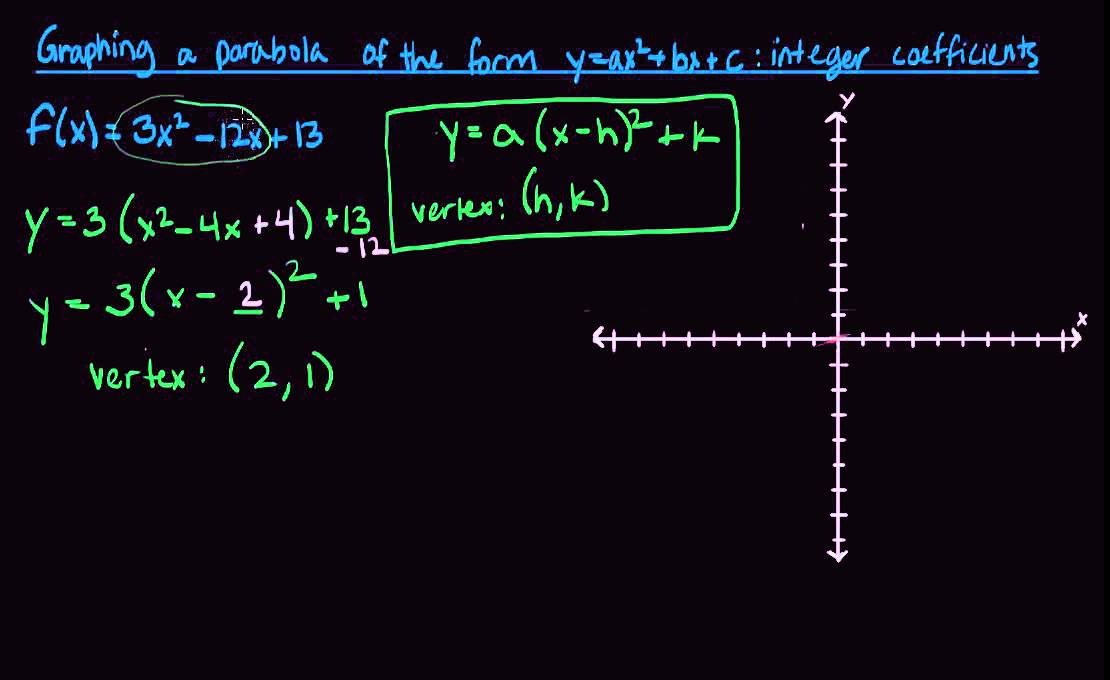



Graphing A Parabola Of The Form Y Ax2 Bx C With Integer Coefficients Youtube
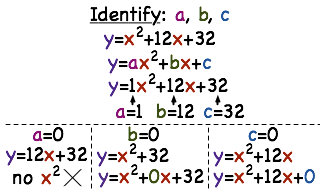



How Do You Find The A B And C Values Of A Quadratic Function Printable Summary Virtual Nerd




Find The Sign Of A B C In Ax 2 Bx C Given The Graph And A Coordinate On It Mathematics Stack Exchange




Number Of A Parabola Of The Form Y Ax 2 Bx C With A 0 Intersection S Of These Graph Of F X 1 X 2 4 Number Of A Possible Distinct Intersection S Of These Graph Is
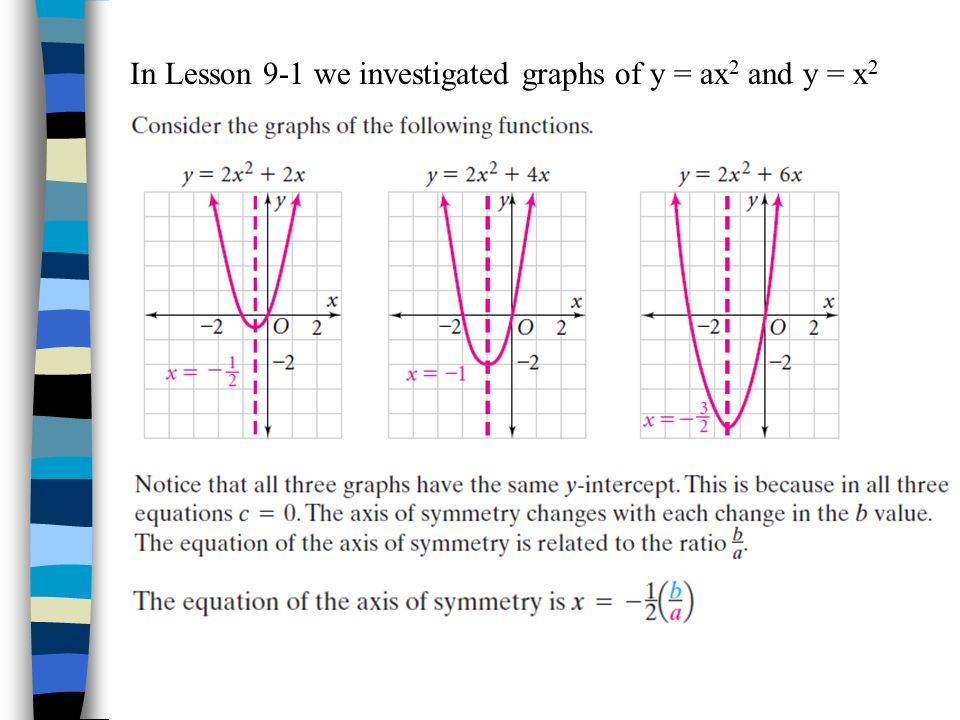



Lesson 9 2 Graphing Y Ax Bx C Objective To Graph Equations Of The Form F X Ax Bx C And Interpret These Graphs Ppt Download



Assignment 2




5 1 Quadratic Functions Functions Siyavula




Ppt The Graph Of A Quadratic Function Powerpoint Presentation Free Download Id



To Investigate The Effect Of The Constants A B And C On The Graph Y Ax2 Bx C Gcse Maths Marked By Teachers Com



Quadratic Relations Y Ax 2 Bx C Between The A N B P And Download Scientific Diagram



1




Finding The Inverse Of Y Ax2 Bx C By Completing The Square Youtube



The Adjoining Figure Shows The Graph Of Y Ax2 Bx C Which Of The Following Statements Is Tru Forums




Y Ax2 Bx C Quadratic Function Ppt Download



Unique Quadratic Equation In The Form Y Ax 2 Bx C




Use The Graph Of Y Ax2 Bx C To Solve A Chegg Com



Solution Find The Values Of A B And C Such That The Equation Y Ax2 Bx C Has Ordered Pair Solutions 3 23 1 9 And 3 5
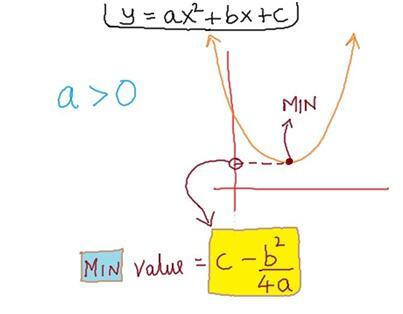



Math Life Quadratic Equation Minimum Value Of Y Ax 2 Bx C Is Y C B 2 4a And Sign Of A Is Positive Http T Co Txzvfe3hnm




Quadratic Equation Handwiki




Misc 7 Find Derivative 1 Ax2 Bx C Chapter 13 Ncert



The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora




Solved The Diagram Shows The Graph Of Y Ax2 Bx C Then A 0 B 0 Self Study 365
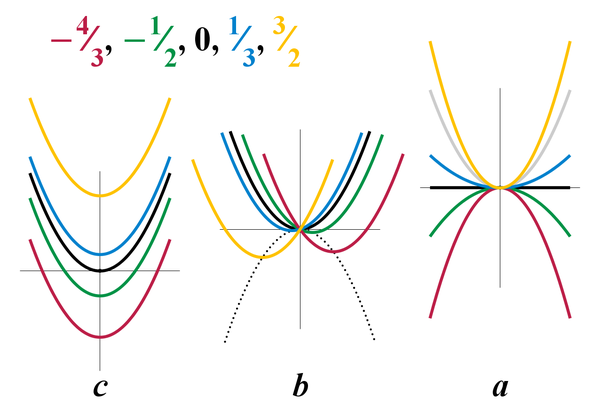



Quadratic Equation Wikiwand
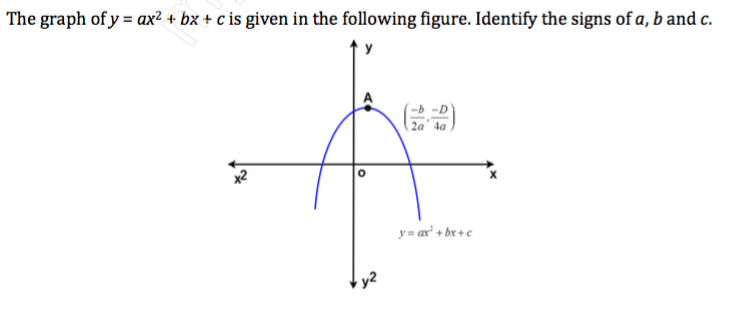



The Graph Of Y Ax 2 Bx C Is Given In The Chegg Com
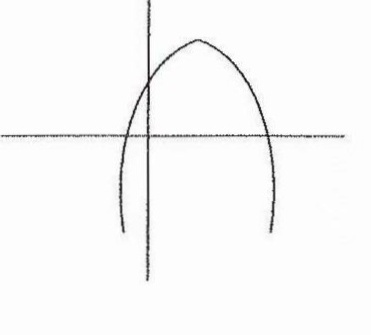



Above Is The Graph Of The Function Y Ax 2 Bx C Where A B 0 And C 0 Which Of The Graphs Below Could Be The Graph Of The Function Y Ax 2 Bx C A B C D E




Quadratic Function Y Ax 2 Bx C Quadratic



Http Www Cardinalspellman Org Ourpages Auto 11 3 28 Roles of a b c Pdf
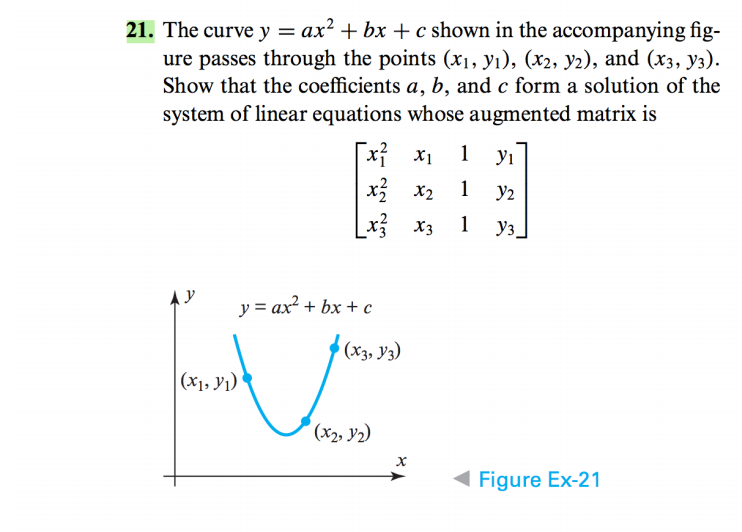



The Curve Y Ax 2 Bx C Shown In The Accompanying Chegg Com



Quadratics



Equations And Graphs




Act Math Practice Question 160 Answer And Explanation Crackact Com
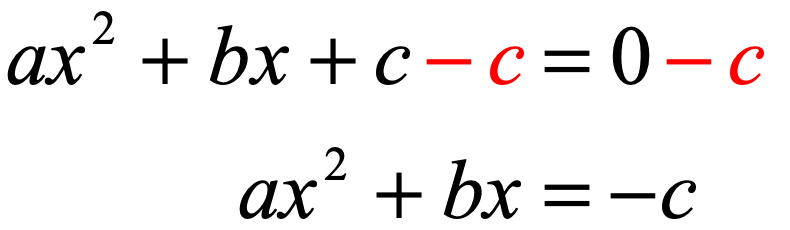



Derive Quadratic Formula Chilimath



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola
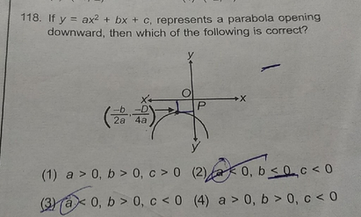



118 If Y Ax2 Bx C Represents A Parabola Opening Downward Scholr



Quadratic Function Y Ax 2 Bx C Quadratic




Quadratic Formula Wikipedia



Solved Use A System Of Equations To Find The Parabola Of The Form Y Ax2 Bx C That Goes Through The Three Given Points 4 77 4 53 2 11 Th Course Hero




Y Ax2 Bx C Three X Y Data Points 30 4



Algebra 1 Activity Sheet Understanding How B Affects The Graph Of Y Ax 2 Bx C



Quadratic Equations Definition Examples Expii




B Value Definition Explanation Video Lesson Transcript Study Com



The Quadratic Formula Explained Purplemath




Example 3 Graph A Function Of The Form Y Ax 2 Bx C Graph Y 2x 2 8x 6 Solution Identify The Coefficients Of The Function The Coefficients Ppt Download




Form The Differential Equation From The Following Primitives Where Constants Are Arbitrary Y A X 2 B X C
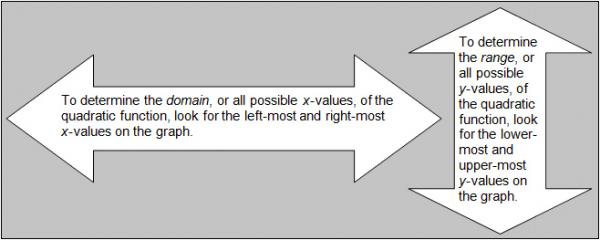



Determining The Domain And Range For Quadratic Functions Texas Gateway



0 件のコメント:
コメントを投稿