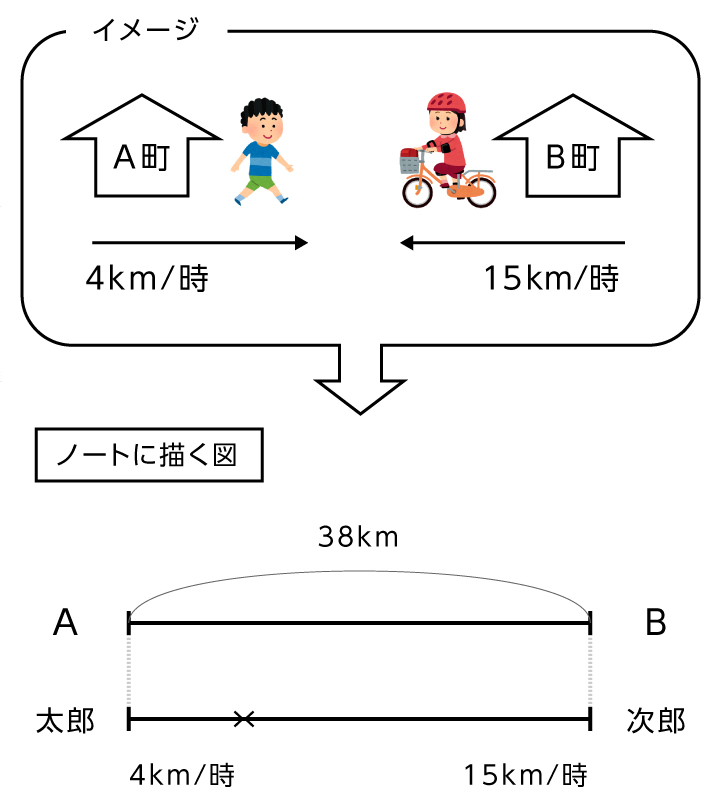
調べたら公式があるようで、 『出会うまでの時間=2地点の距離÷速さの和』 と書いてありましたが、 なぜこのような公式になるのか、理解できません。 今回は出会う旅人算の解き方・考え方です。 他の旅人算の問題&解説は旅人算のまとめページをご覧下さい。 問題 2400m離れた地点から、さとし君とたかし君が向かい合って同時に出発します。さとし君は毎分55m、たかし君は毎分65mで歩きます。2人は出発して 解答と解説 2台の自動車が1時間に移動する距離の合計は、 24 48 = 72 24 48 = 72 A A 地点と B B 地点の間の距離 (2台の自動車が出会うまでに進んだ距離の合計)は 108 k m 108 k m 、2台の自動車の移動した距離の和は1時間ごとに 72 k m 72 k m ずつ増加するので、2台の自動車がすれ違うまでにかかる時間は、 108 ÷ 72 = 15 108 ÷ 72 = 15 求める答えは、2台の自動車がすれ違っ
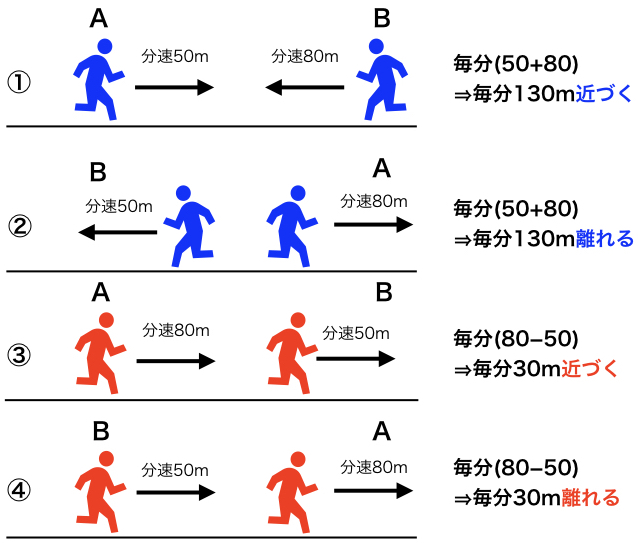
旅人算 わかりやすい出会い算と追いつき算の解き方を簡単計算 Landgather
出会い算 解き方
出会い算 解き方-仕事算に類似の問題として出会い算が考えられる。 出会い算 は、2人が 協力して一定の道のりを歩くという仕事 をすることとみなせるからであり、その意味で、 ニュートン算 は 追いつき旅人算 とみな 旅人算の問題16題をただひたすら解くページ! 解き方もあり〼 中学受験算数の中でも、 苦手な人が最も多い単元の一つと言っていいのが、この旅人算 。 問題のバリエーションも難易度も様々 で、取り組みにくいという点も特徴ですね。 そこで、旅人算




状況図とダイヤグラムどちらを書くべき 家庭教師としの勉強部屋
そこで、 1 1 分間が経過しました。 すると、女の人は分速 80 80 (m)、旅人は分速 60 60 (m)で進むので、二人で合わせて 80 60 = 140 80 60 = 140 (m)進んだことになります。 よって、二人の間のキョリも、 4 − 140 = 280 4 − 140 = 280 (m)まで縮まります。 したがって、 1 1 分経過するごとに 140 140 (m)キョリが縮まるので、 4 ÷ 140 = 3 ( 分) 4 ÷ 140 = 3 ( 分) つ中学受験に必須な定番特殊算とその解き方を90分で全て学ぼう! 収録時間9時間の超力作! ! ぜひお役立てください! ! 毎日少しずつ中学 旅人算追いつく問題の解き方まとめ! お疲れ様でした! 2人が追いつくという問題を解くためには、2人の道のりが縮まっていくという発想が大切です。 2人の速さを見比べると、1分間でどれくらいずつ道のりが縮まるのかが分かります。 そこから、どのくらいの時間で追いつくのかを
160=60(ナミさんとお兄さんの速度の違い) 360÷60=6 答え 兄さんはナミさんに6分後に追いつく 確かめ ナミさん×6=7(道のり) お兄さん1×6=7(道のり) 最後に 「変わり方を調べて(1)」の勉強は、 表を使って変化のきまり をみつけ、それを式に表して問題を解くことをねらいとしています。 そこで問題の解き方を説明する時の表を用いた考え方や覆面算の解き方ヒント 桁の繰り上がりに注目 各位の計算を式にして、これらを満たすように 表を使って当てはまる数を調べる。 その他の工夫 同じ形の枠を用意する 使用文字一覧を作る 残り数字チェックを常にする アルファベットを利用する 移項して計算すると、 380x=5700 両辺を380で割ると、 x=15 解
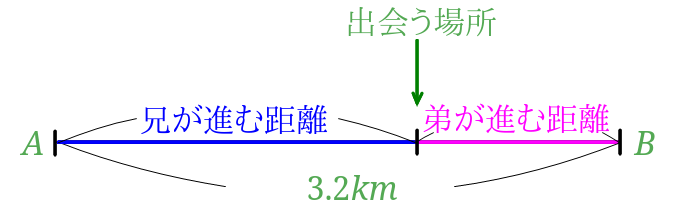
今回は池の周りで出会う旅人算の解き方・考え方です。 他の旅人算の問題&解説は旅人算のまとめページをご覧下さい。 問題 さとし君とたかし君が池の周りを同じ地点から反対方向に同時に進みます。2人は7分後にはじめて出会いました。池の周りの長さ つまり、2人が出会うというのは、2人の進んできた道のりの合計が3300mになったときということです。 では次に、2人はどれくらいのペースで進んでいっているのかを考えます。 AくんとBさんが出発してから1分後の状況を考えてみましょう。 Aくんは分速60mだから、60m進んでおり Bさんは分速50mだから、50m進んでいます。 つまり、 1分後には2人合わせて110m進んだこと 和差算の解き方を押さえておくのは,合格のために大いに意味があります。 和差算の解き方! それではここからは 和差算の解き方 について,例題を交えつつ復習していきましょう。 りんごとみかんがいくつかあります。りんごはみかんより3個多く,全部




旅人算の基本 図をかいて整理しよう




旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学
流水算 中学受験 2そうの船 は, A町から何kmのところで出会い ました か。 問題6の答え (1) 毎時2.5km (2) 18km 解説 1/13 まず,それぞれの船の速さを求めましょ う。 A船は川上の町 を, B船は川下の町を同時に出発 し, 向かい合って進みまし た。 出発してから2時間後に2そうの船は出会 い油分け算の解き方 25 35 Author 松本卓也 Created Date PM 年齢算の解き方 1 年齢算 大人塾 1 年齢算とは、年齢にまつわる計算です。 頑張って解いていきましょう! 2 年齢差は、 何年経っても何年前でも変わらない 年齢算のポイントは当たり前なことのように 感じますが、とても重要なことです。例題を やってみましょう。 ポイント 3 現在の母の



遅れて出発して出会う旅人算の解き方 考え方 算数パラダイス




小6 速さ 旅人算 小学生 算数のノート Clear
時計算のポイント3つ 時計算とは? 時計算の解き方・テクニックは「55度」!「旅人算」の追いつき算 時計は全体で360度・5分ごとに30度(360÷12) 時計算:長針と短針の進むスピード・角度 (基本)時計算の問題パターン 1 「時計の長針と短針が重なる「第491回 合否を分ける問題の解き方 流水算」 中学入試の算数の問題は、基本的な学力を測る問題(=基本問題)、問題文の意味や条件の理解、条件の使い方が問われる問題(=応用問題)、難度の高い問題(=発展問題)の3段階で構成されていることが一般的です。 鶴亀算(つるかめ算)の解き方 計算で解く方法と面積図で解く方法の教え方を画像を使って解説しています。 和差算(わさざん)の解き方 タイトルとurlをコピーしました
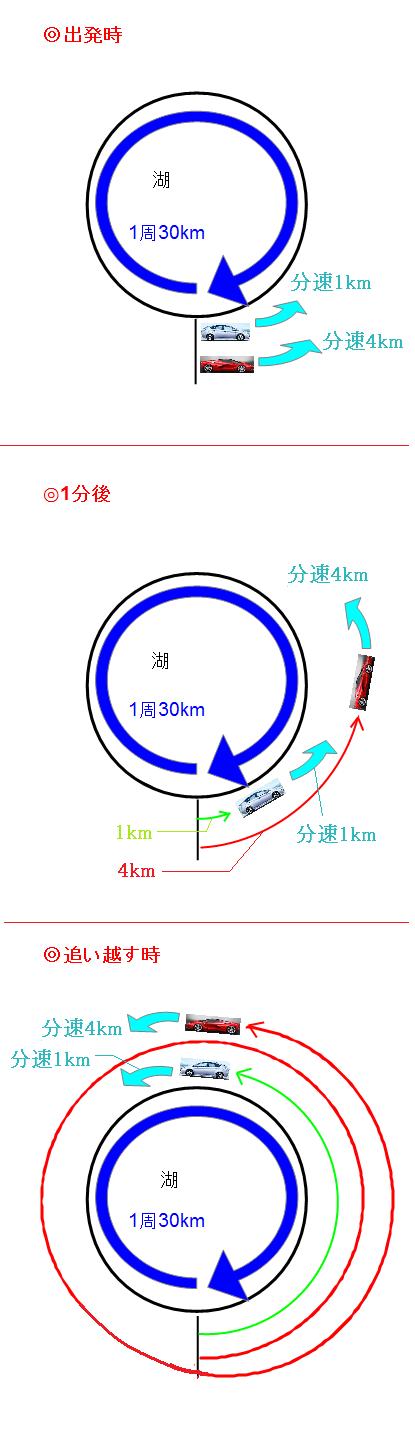



旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける




旅人算の苦手を克服 分かりやすく教える方法と解き方はコレ みけねこ小学校
(2)bとcは何分ごとに出会いますか。( 分) (大阪桐蔭中 08年 ユニーク入試) <問題1の考え方と答え> 旅人算の問題のパターンに、池や遊歩道のような「周」を回るものと、ある区間を往復するという2つがあります。入試には頻繁(ひんぱん)に出題されています。 この機会に教え方1 変化する様子を表にかいて、変化の変わり方(一定量が増えていくこと)をみつけ、問題の解き方をとらえさせます。 下の問題を例にして、考えさせます 上の問題は出会い算などとも呼ばれています 問題を読ませた後に、問題の場面をとらえさせます↓ 変化の様子を表に整理させます↓ 下の表から、 1分たつごとに 、リカさんとお兄さんの歩いた道のり旅人算に関する問題の解き方一覧 <旅人算の基本1> (1) 分速85mで歩く人と分速65mで歩く人が,それぞれA,B両地点から向かい合って同時に出発すると18分後に出会います。 ・・・ (2) 家から駅までは10mです。 姉が駅から家へ分速80mで,妹は家から駅へ
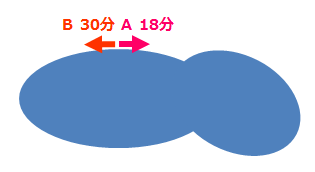



道のり 距離 が問題文にない旅人算の解き方



Q Tbn And9gcsfsd7mqbjlmrw6l1hx01w9aoyekjuqluvpeyoagxi Aqwfb3zo Usqp Cau
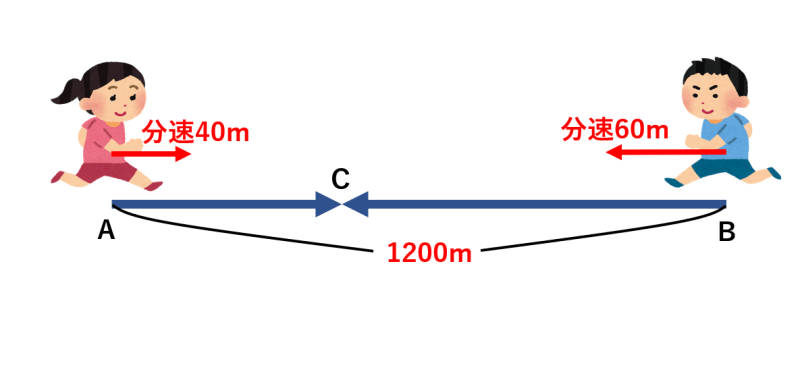
「速さ」の公式と問題の解き方のポイント|小学生に教えるための解説 管理人 10月 12, 18 / 12月 3, 18 小学6年生で習う算数の「速さ」は苦手な子が多く、これが原因で算数が嫌いになってしまう子も少なくありません。 たしかに「速さ」の問題を解く際にはいくつかポイントがあり、これら旅人算は、 「二人の間の距離や、出会ったり・追いついたりする時間」 を求めるものなので、 「旅人算」の解き方のポイント・テクニックは、 1 2人の間の距離を考える 2 速さの和または差のどちらになるかを考える の二点になります。その上で「線分図旅人算の解き方 中学受験の算数で出てくる旅人算について解説しています。 最も基本となる旅人算の問題はお互いに向かって進んでいる(旅をしている)二人がいつ出会うかというものです。 問題文には二人のあいだの距離とそれぞれの進む速さ(スピード)が提示されていて、ここから出会う時間を求めるというものです。 具体的には、このような問題です
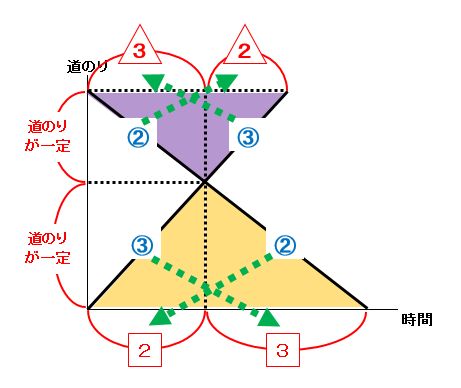



速さと比 ダイヤグラムで旅人算を図形的に考える 基本編 ページ 3 みみずく戦略室




旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学
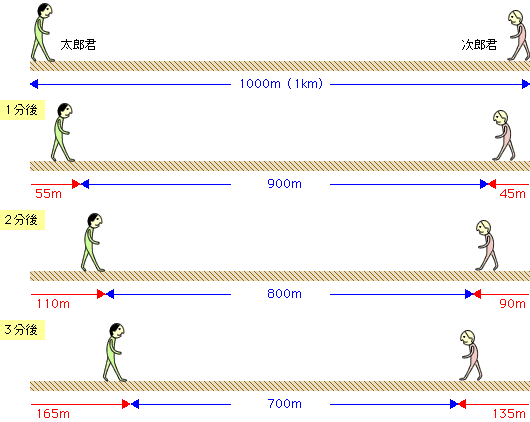
出会い算の変則的な問題です。 はじめて解くタイプの問題で解き方の方針が分からなくても、図に書いて整理すれば自然と解き方が見えてくると思います。 解法は主に2つあるのでそれぞれ見ていきましょう。 解法1旅人算① 出会う旅人算の解き方 ここでは、2人が別々の地点から逆向き出発して、出会うまでの時間を求める旅人算の解き方を解説します。 少し前にも書きましたが、出発時とゴール時の状況、1分後(1時間後、または1秒後)の状況を考えるのがコツです。 方陣算の記事一覧 方陣算まとめ(この記事) 中実方陣 中空方陣 三角形に並べる 多角形に並べる「方陣算」を学習している中学受験生の方「石がたくさん並んでいて面倒くさく、難しそう」と思っていませんか?実は、ちょっとした図を書くだけで方陣算は



遅れて出発して出会う旅人算の解き方 考え方 算数パラダイス
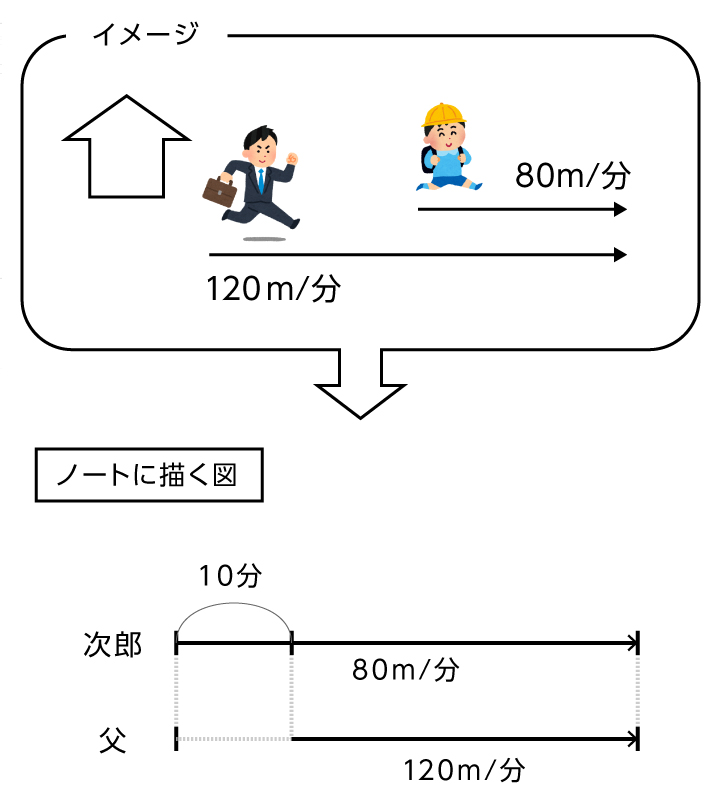



旅人算ってどんなもの 旅人算をわかりやすく解説 中学受験ナビ
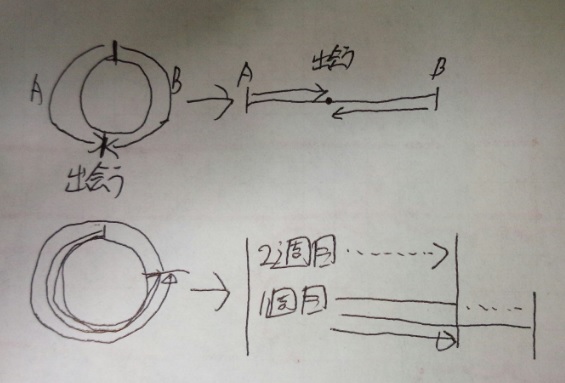
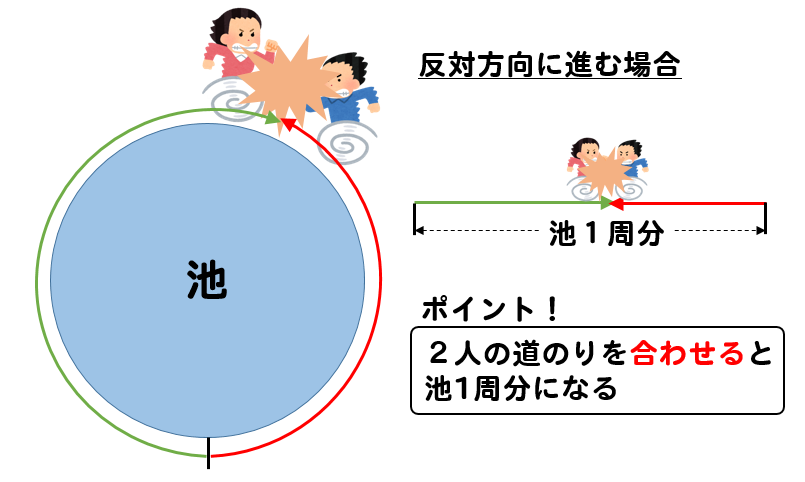
旅人算の池の周りを反対方向にまわる出会い算の解き方とコツ 池の周りを反対向きにまわる出会い算になります。 解法のポイントはその問題の捉え方です。 捉え方を間違えると難問化してしまうので、そうなってしまわないようにしっかり問題を的確にとらえていきましょう。 それではAuthor 松本卓也 Created Date PM




状況図とダイヤグラムどちらを書くべき 家庭教師としの勉強部屋



3人旅人算 Wikipedia



旅人算 出会い算 を算数の解法でお願いします 池のまわりを兄は14分で一周 Yahoo 知恵袋
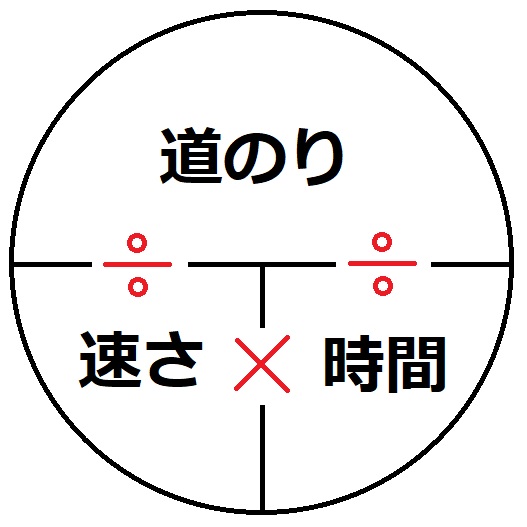



基本 旅人算の解き方 テクニック 中学受験 塾なし の勉強法



旅人算の苦手を克服 分かりやすく教える方法と解き方はコレ みけねこ小学校



旅人算 算数解法の極意



1



1




え こんなに簡単だったの 中学入試の分かりやすい旅人算の解き方 受験ボックス




旅人算 の問題の解き方 小学生に教えるための分かりやすい解説 数学fun




旅人算 問題の解説まとめ それぞれのパターンの解き方は 数スタ




算数文章題講座 旅人算の解き方 基本問題




旅人算の解き方 中学受験の算数教室




旅人算 わかりやすい出会い算と追いつき算の解き方を簡単計算 Landgather




算数文章題講座 旅人算の解き方 基本問題




旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける
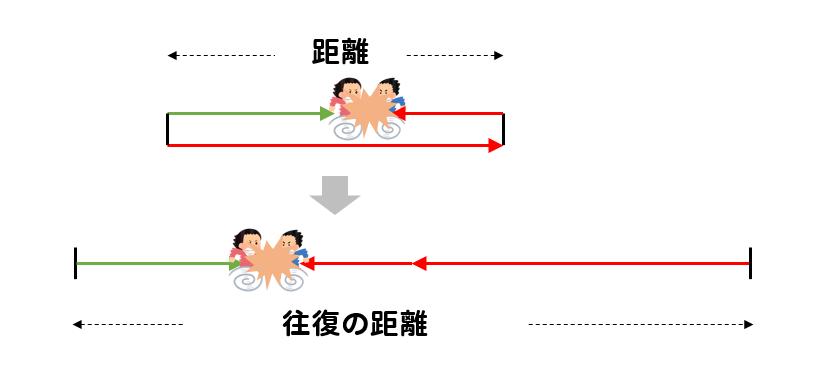



旅人算 往復するときの解き方は 2回目に出会うときは 数スタ
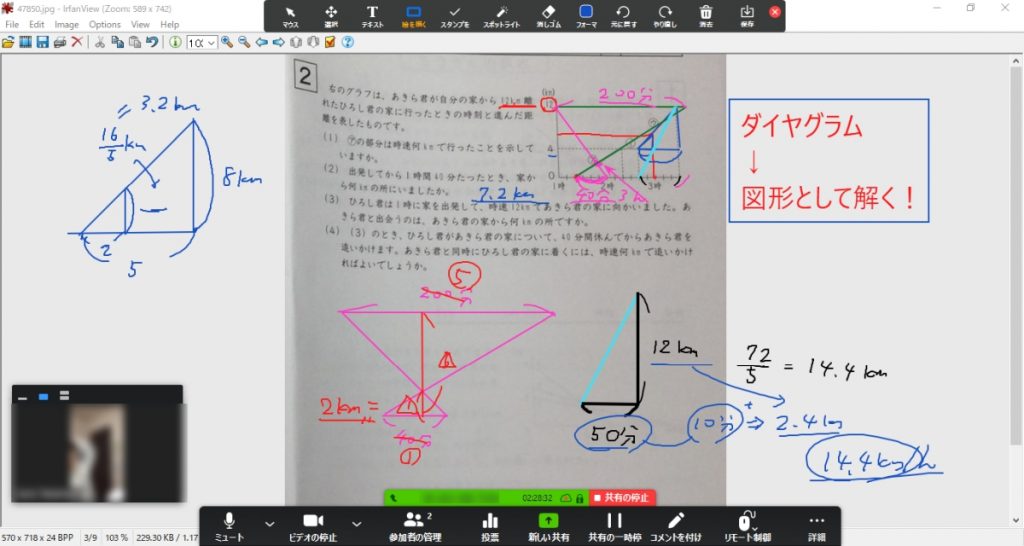



ダイヤグラムを旅人算で解く子は伸びない オンライン授業専門塾ファイ



例題あり 旅人算とは 出会い算 追いつき算など種類別の解き方や教え方のコツも解説 学びtimes



旅人算の問題16題をただひたすら解くページ 解き方もあり〼 チャンプルー




旅人算の基本 図をかいて整理しよう




旅人算の基本 図をかいて整理しよう




旅人算の基本問題 Youtube




3人の旅人算 考え方と解き方




旅人算 2人が追いつく問題の解き方は 数スタ



旅人算の苦手を克服 分かりやすく教える方法と解き方はコレ みけねこ小学校




旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学




旅人算 速さの和と差から出会い算と追い越し算を再考する みみずく戦略室



旅人算の解き方は 作図 で極める 中学受験プロ講師ブログ




え こんなに簡単だったの 中学入試の分かりやすい旅人算の解き方 受験ボックス



1




印刷可能 中学受験 算数 速さ 旅人算




旅人算の基本 図をかいて整理しよう




例題あり 旅人算とは 出会い算 追いつき算など種類別の解き方や教え方のコツも解説 学びtimes




算数文章題講座 旅人算の解き方 基本問題




え こんなに簡単だったの 中学入試の分かりやすい旅人算の解き方 受験ボックス



旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける



旅人算ってどんなもの 旅人算をわかりやすく解説 中学受験ナビ




旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学




旅人算に関する問題の解き方一覧 中学受験の算数 理科ヘクトパスカル




3人の旅人算 考え方と解き方



Spi M54e217p7lcis9d Com Category E9 80 9f E5 Ba A6 E7 Ae 97 E9 80 9a E9 81 8e E7 Ae 97




旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学




旅人算 往復するときの解き方は 2回目に出会うときは 数スタ




6年生算数 変わり方を調べて 旅人算がアニメでわかる いっちに算数 のブログ




旅人算の基本 図をかいて整理しよう



旅人算 応用 速い方が遅い方より池一週分多く周って



旅人算 算数の教え上手 学びの場 Com



旅人算 問題の解説まとめ それぞれのパターンの解き方は 数スタ




5年算数 表を使って考えよう 出会い算 追いつき算 Youtube




旅人算 の問題の解き方 小学生に教えるための分かりやすい解説 数学fun



旅人算 算数の教え上手 学びの場 Com



中学受験 旅人算とは 基本公式から往復など応用問題 ダイヤグラムまで そうちゃ式 受験算数 2号館 図形 速さ




往復の旅人算 折り返して出会い そうちゃ式 線分図 面積図 矢印図 状況図 ダイヤグラムで中学受験を楽しく得意に
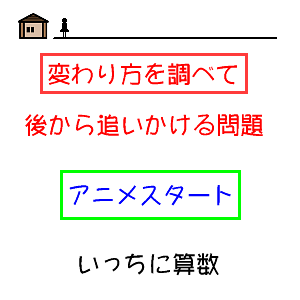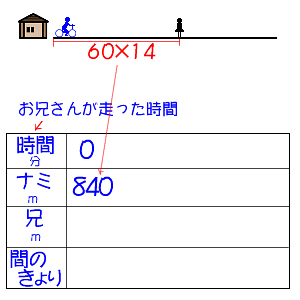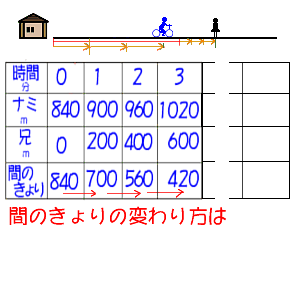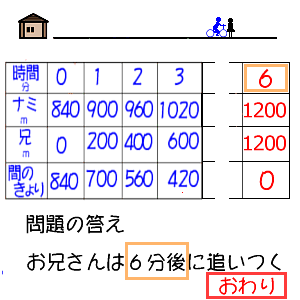



6年算数 変わり方を調べて 1 出会い算




中学受験 特殊算は何種類ある 算数の文章題の見分け方 かるび勉強部屋 中学受験 勉強 算数



旅人算の問題16題をただひたすら解くページ 解き方もあり〼 チャンプルー




算数文章題講座 旅人算の解き方 基本問題




旅人算 の文章問題 計算ドリル 問題集 数学fun




状況図とダイヤグラムどちらを書くべき 家庭教師としの勉強部屋
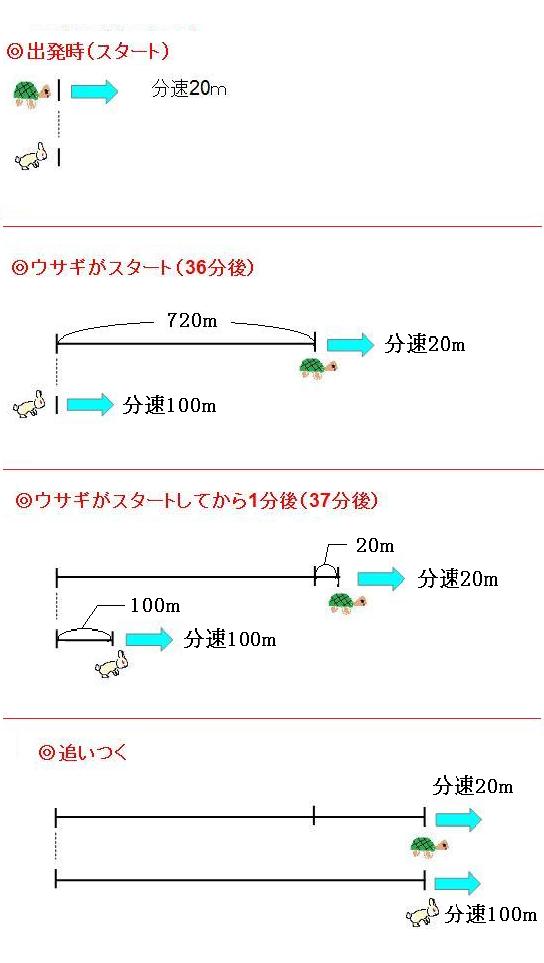



旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける




旅人算の基本 図をかいて整理しよう



旅人算の目次 公式なんか不要 基本6パターンの解説 算数パラダイス
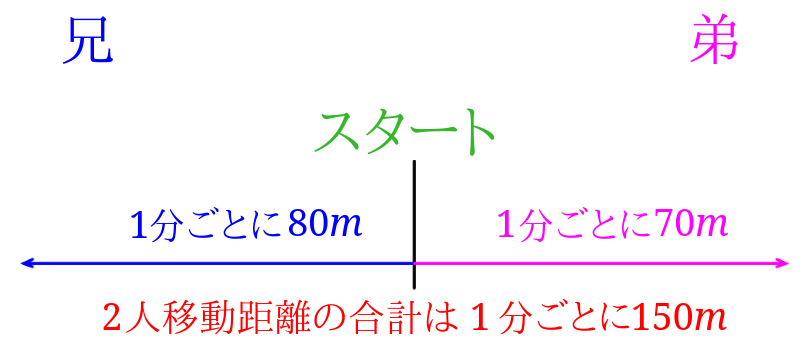



旅人算の苦手を克服 分かりやすく教える方法と解き方はコレ みけねこ小学校




旅人算 Wikipedia
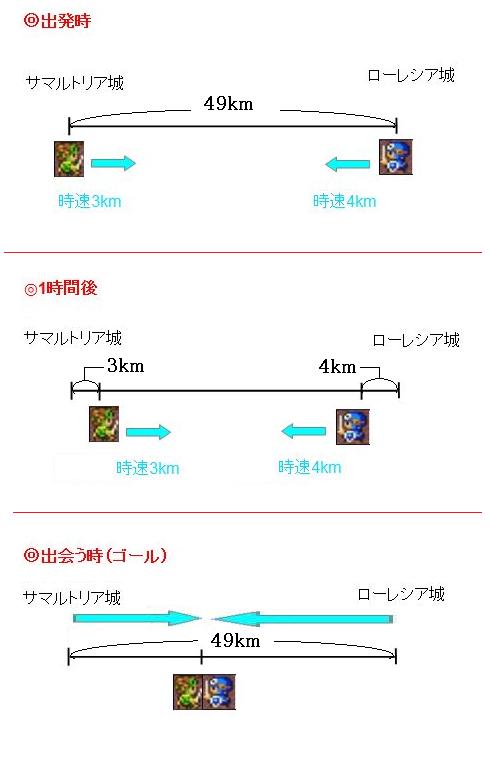



旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける



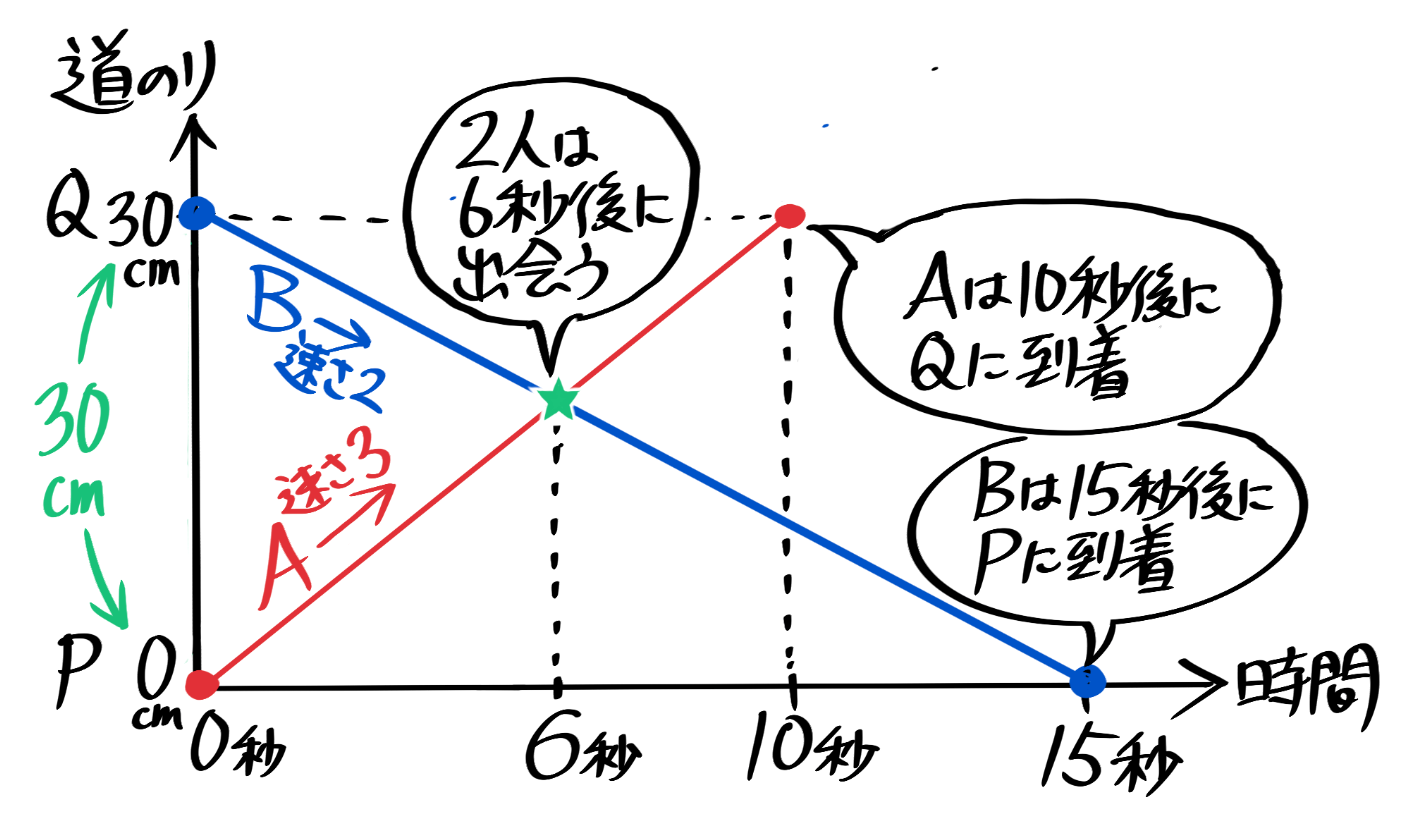
旅人算で間違いやすいポイントはココ




旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学



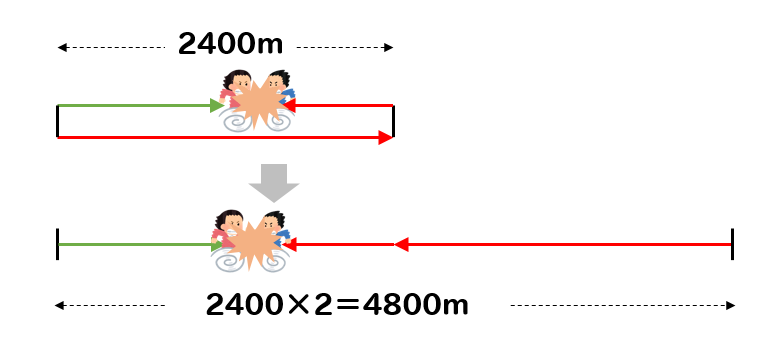
中学受験 旅人算とは 基本公式から往復など応用問題 ダイヤグラムまで そうちゃ式 受験算数 2号館 図形 速さ




旅人算の解き方まとめ 公式から応用問題3選までわかりやすい解説 中学受験算数 遊ぶ数学




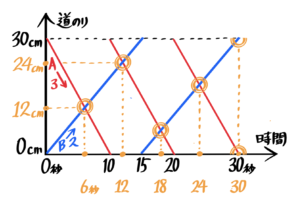
グラフが登場する旅人算の解き方を問題集形式でご紹介




旅人算 の問題の解き方 小学生に教えるための分かりやすい解説 数学fun




旅人算の問題と解き方その1 2人が 分後に出会う Irohabook



旅人算 出会い算 を算数の解法でお願いします 池のまわりを兄は14分で一周 Yahoo 知恵袋



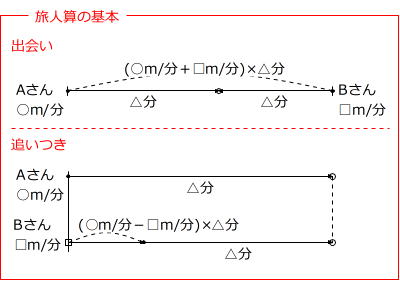
旅人算 問題の解説まとめ それぞれのパターンの解き方は 数スタ




例題あり 旅人算とは 出会い算 追いつき算など種類別の解き方や教え方のコツも解説 学びtimes




速さ問題の解き方 旅人算 通過算 流水算 算数が伸びないわけ 算数を伸ばす勉強法



第492回 合否を分ける問題の解き方 旅人算 前田昌宏の中学受験が楽しくなる算数塾
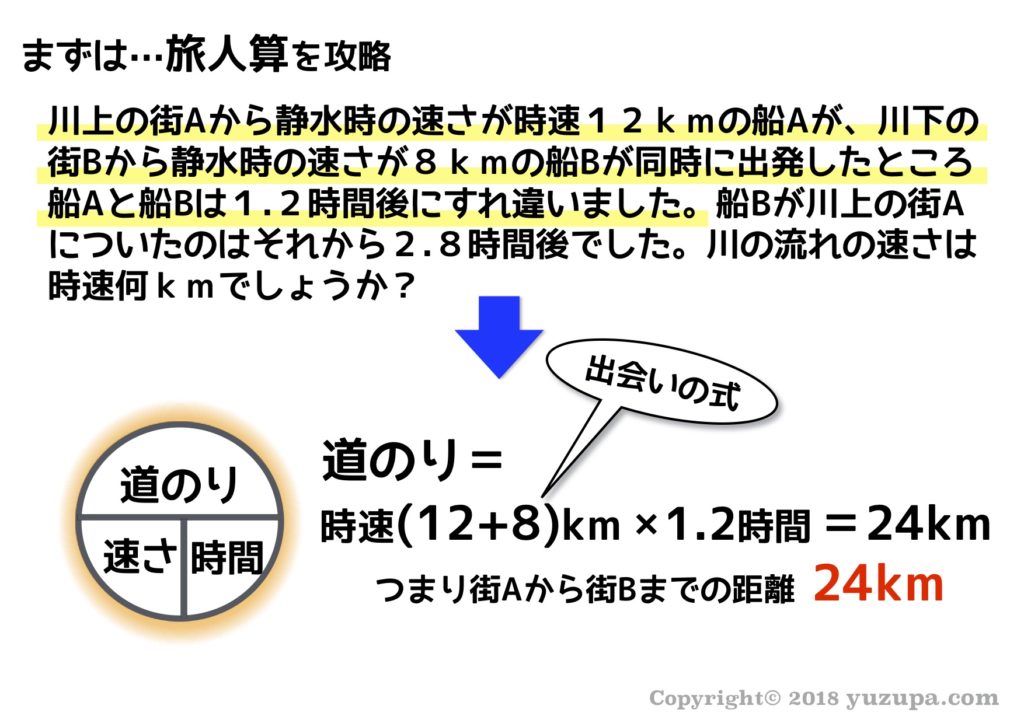



中学受験 流水算は 4つ速さを整理すれば簡単に解ける かるび勉強部屋




旅人算の基本公式をマスター




旅人算の苦手を克服 分かりやすく教える方法と解き方はコレ みけねこ小学校




中学受験頻出 仕事算 の3種類の解き方を図で分かりやすく解説 数学fun
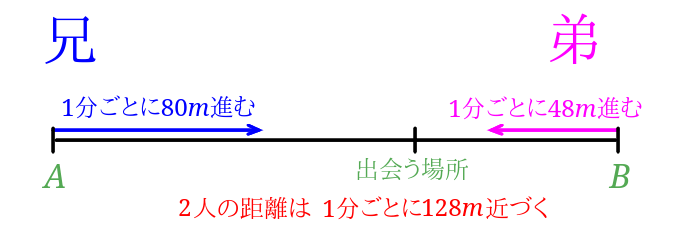



旅人算の苦手を克服 分かりやすく教える方法と解き方はコレ みけねこ小学校
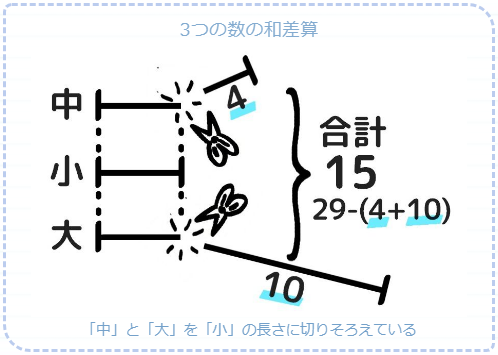



和差算プリント57枚 基本公式の覚え方から応用 発展問題の解き方まとめ 中学受験 そうちゃ式 受験算数 新1号館 数論 特殊算




旅人算 の問題の解き方 小学生に教えるための分かりやすい解説 数学fun




旅人算の4つの出題パターンを解説 1分後を意識すればすべて解ける




旅人算の解き方 中学受験の算数教室




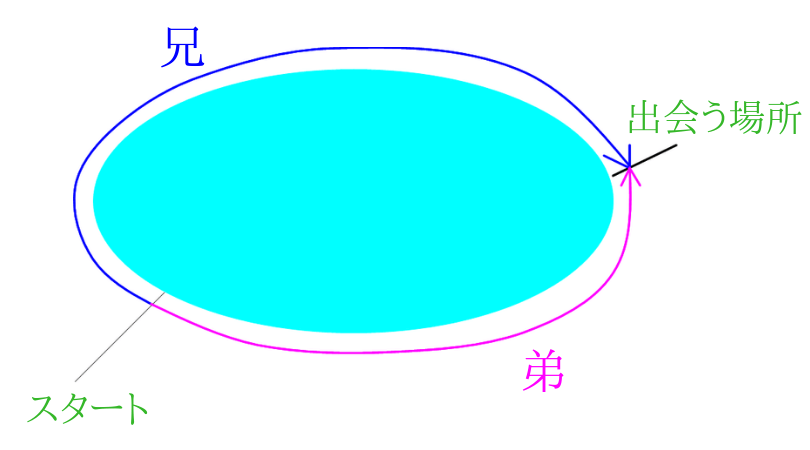
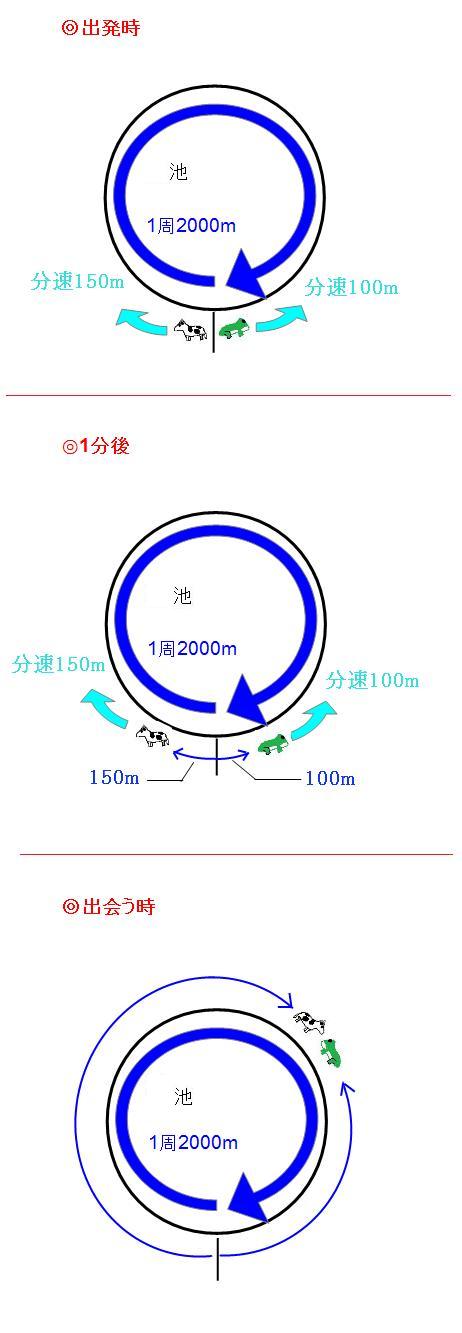
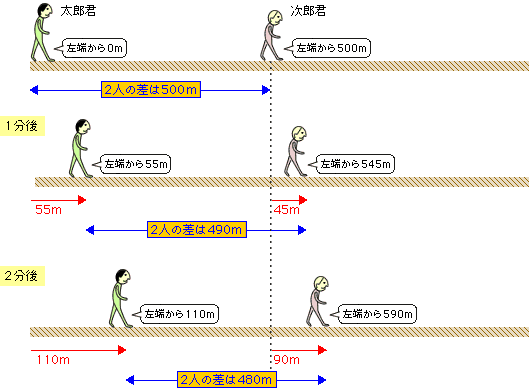
旅人算 池の周りで出会う問題の解き方 考え方 算数パラダイス




算数文章題講座 旅人算の解き方 基本問題
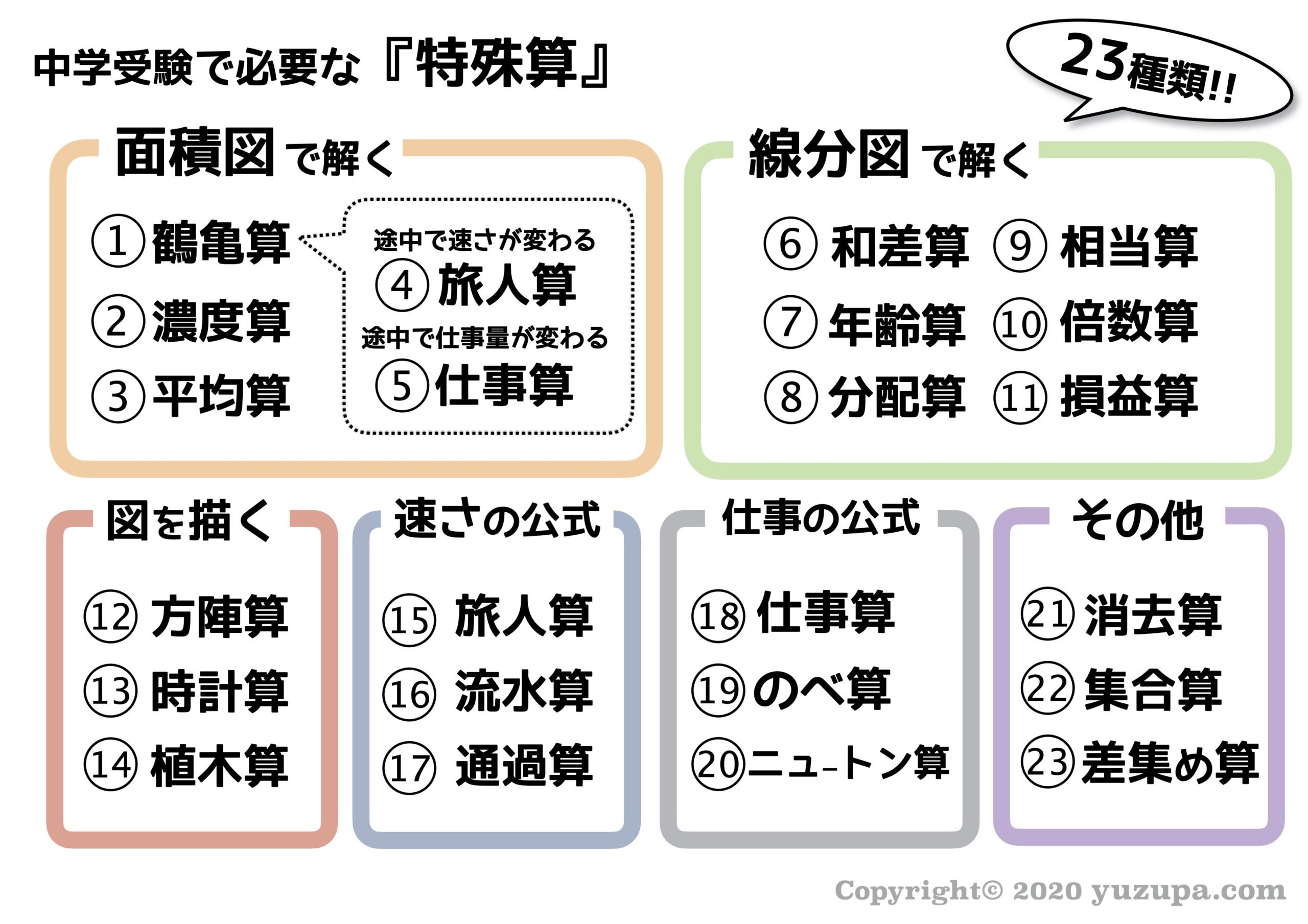



中学受験 特殊算は何種類ある 算数の文章題の見分け方 かるび勉強部屋



旅人算 わかりやすい出会い算と追いつき算の解き方を簡単計算 Landgather
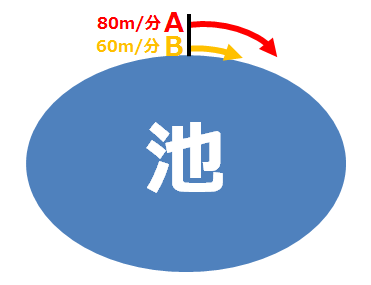



旅人算 池の周りを回る二人が出会う問題 の解き方



0 件のコメント:
コメントを投稿